Area under curve CIE)

$\def\D{\displaystyle}$

1 (CIE 2012, s, paper 11, question 11either)

The diagram shows part of the curve $\D y = 9x^2 - x^3,$ which meets the x-axis at the origin $\D O$ and at the point $\D A$. The line $\D y - 2x + 18 = 0$ passes through $\D A$ and meets the y-axis at the point $\D B.$
(i) Show that, for $\D x \ge  0, 9x^2 - x^3 \le  108.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the line $\D AB$ and the y-axis. [6]

2 (CIE 2012, s, paper 11, question 11or)

The diagram shows part of the curve $\D y = 2\sin 3x .$ The normal to the curve $\D y = 2\sin 3x$ at the point where $\D x = \frac{\pi}{9}$ meets the y-axis at the point $\D P.$
(i) Find the coordinates of $\D P.$ [5]
(ii) Find the area of the shaded region bounded by the curve, the normal and the y-axis. [5]

3 (CIE 2012, s, paper 22, question 11either)

The diagram shows part of the curve $\D y = \sin\frac{1}{2}x.$  The tangent to the curve at the point $\D P\left(\frac{3\pi}{2},\frac{\sqrt{2}}{2}\right)$  cuts the x-axis at the point $\D Q.$
(i) Find the coordinates of $\D Q.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the tangent and the x-axis. [7]

4 (CIE 2012, s, paper 22, question 11or)
(i) Given that $\D y = xe^{-x},$ find $\D \frac{dy}{dx}$  and hence show that $\D \int xe^{-x}dx=-xe^{-x}-e^{-x}+c.$  [4]

The diagram shows part of the curve $\D y = xe^{-x}$ and the tangent to the curve at the point $\D R\left(2,\frac{2}{e^2}\right).$
(ii) Find the area of the shaded region bounded by the curve, the tangent and the y-axis. [7]

5 (CIE 2012, w, paper 11, question 12either)

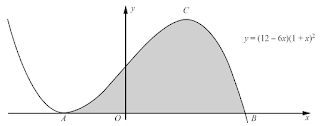
The diagram shows part of the graph of $\D y = (12 - 6x)(1 + x)^2,$ which meets the x-axis at the points $\D A$ and $\D B.$ The point $\D C$ is the maximum point of the curve.
(i) Find the coordinates of each of $\D A, B$ and $\D C.$ [6]
(ii) Find the area of the shaded region. [5]

6 (CIE 2012, w, paper 11, question 12or)

The diagram shows part of a curve such that $\D \frac{dy}{dx} = 3x^2 - 6x - 9.$ Points $\D A$ and $\D B$ are stationary points of the curve and lines from $\D A$ and $\D B$ are drawn perpendicular to the x-axis. Given that the curve passes through the point (0, 30), find
(i) the equation of the curve, [4]
(ii) the x-coordinate of $\D A$ and of $\D B,$ [3]
(iii) the area of the shaded region. [4]

7 (CIE 2012, w, paper 13, question 11either)
The tangent to the curve $\D y = 5e^x + 3e^{-x}$ at the point where $\D x = \ln\frac{3}{5},$ meets the x-axis at the point $\D P.$
(i) Find the coordinates of $\D P.$ [5]
The area of the region enclosed by the curve $\D y = 5e^x + 3e^{-x},$ the y-axis, the positive x-axis and
the line $\D x = a$ is 12 square units.
(ii) Show that $\D 5e^{2a} - 14e^a - 3 = 0.$ [3]
(iii) Hence find the value of $\D a.$ [3]

8 (CIE 2012, w, paper 22, question 12or)

The diagram shows part of the curve $\D y = 8 + e^{-\frac{x}{3}}$  crossing the y-axis at $\D P.$ The normal to the curve at $\D P$ meets the x-axis at $\D Q.$
(i) Find the coordinates of $\D Q.$ [4]
The line through $\D Q,$ parallel to the y-axis, meets the curve at $\D R$ and $\D OQRS$ is a rectangle.
(ii) Find $\D \int \left(8+e^{-\frac{x}{3}}\right)dx$   and hence find the area of the shaded region. [6]

9 (CIE 2013, w, paper 13, question 6)
Do not use a calculator in this question.

The diagram shows part of the curve $\D y= 4- x^2.$
Show that the area of the shaded region can be written in the form $\D \frac{\sqrt{2}}{p},$  where $\D p$ is an integer to
be found. [6]

10 (CIE 2013, w, paper 21, question 11)

The diagram shows part of the curve $\D y= e^{\frac{x}{3}}.$ The tangent to the curve at $\D P(9,e^3),$  meets the
x-axis at $\D Q.$
(i) Find the coordinates of $\D Q.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the coordinate axes and the tangent
to the curve at $\D P.$ [6]

11 (CIE 2014, s, paper 12, question 4)
The region enclosed by the curve $\D y = 2 \sin 3x,$ the x-axis and the line $\D x = a ,$ where
$\D 0<a<1$ radian, lies entirely above the x-axis. Given that the area of this region is $\D \frac{1}{3}$  square unit,
find the value of $\D a.$ [6]

12 (CIE 2014, s, paper 13, question 11)

The diagram shows the graph of $\D y = \cos 3x + \sqrt{3} \sin 3x,$ which crosses the x-axis at $\D A$ and has a maximum point at $\D B.$
(i) Find the x-coordinate of $\D A.$ [3]
(ii) Find $\D \frac{dy}{dx}$ and hence find the x-coordinate of $\D B.$ [4]
(iii) Showing all your working, find the area of the shaded region bounded by the curve, the x-axis
and the line through $\D B$ parallel to the y-axis. [5]

13 (CIE 2014, w, paper 13, question 11)

The diagram shows part of the curve $\D y=(x+5)(x-1)^2.$
(i) Find the x-coordinates of the stationary points of the curve. [5]
(ii) Find $\D \int (x+5)(x-1)^2dx.$ [3]
(iii) Hence find the area enclosed by the curve and the x-axis. [2]
(iv) Find the set of positive values of $\D k$ for which the equation $\D (x+5)(x-1)^2=k$  has only one real solution. [2]

14 (CIE 2014, w, paper 21, question 12)
(i) Show that $\D x-2$ is a factor of $\D 3x^3-14^2+32.$
(ii) Hence factorise $\D 3x^3-14x^2+32$ completely.

The diagram below shows part of the curve $\D y =3x-14+\frac{32}{x^2}$  cutting the x-axis at the points $\D P$ and $\D Q.$
(iii) State the x-coordinates of $\D P$ and $\D Q.$ [1]
(iv) Find $\D \int (3x-14+\frac{32}{x^2})dx$  and hence determine the area of the shaded region. [4]

Answers
1. (ii) $\D  628$
2. (i) $\D (0, 1.58)$
(ii) $\D 0.292$
3. (i) $\D x = 2 + \frac{3\pi}{2}$
(ii) $\D \frac{3\sqrt{2}}{2}-2$
4.  $\D (9/e^2) - 1$
5. (i) $\D A(-1, 0),B(2, 0), C(1, 24)$
(ii) $\D 40.5$
6. (i) $\D y = x^3 - 3x^2 - 9x + 30$
(ii) $\D x = -1, 3$
(iii) $\D 76$
7. (i) $\D P(3.49, 0)$
(ii)
(iii) $\D \ln 3$
8. (i) $\D Q(-3, 0)$
(ii) $\D 8x - 3e^{-\frac{x}{3}}, A = 3$
9.  $\D \frac{\sqrt{2}}{3}$
10. (i) $\D (6, 0)$
(ii) $\D 27.1$
11.  $\D a =\frac{\pi}{9}$
12. (i) $\D x = \frac{5\pi}{18}$
(ii) $\D \frac{dy}{dx} =   3\sqrt{3} \cos 3x - 3 \sin 3x$
(iii) $\D A = \frac{2}{3}$
13. (i) $\D x = 1,-3$
(ii) $\D \frac{x^4}{4}+x^3- \frac{9x^2}{2}+5x.$
(iii)  $\D 108$ (iv) $\D k > 32$
14. (ii) $\D (x - 2)(x - 4)(3x + 4)$
(iii) $\D x = 2, 4,$
(iv) $\D 2$